Dimensi Tiga II: Kedudukan Titik, Garis, dan Bidang dalam Ruang
1. Kedudukan titik terhadap garis
Sebuah titik dapat terletak di sebuah garis atau di luar garis. Jika titik terdapat di sebuah garis maka jarak titiknya 0 dan jika titik terletak di luar garis jaraknya dihitung tegak lurus terhadap garis.

Contoh, pada gambar di atas diketahui sebuah titik B terhadap garis g. Titik B memiliki jarak terhadap garis g sejauh garis putus-putus (B ke B’) dimana B’ merupakan proyeksi tegak lurus titik B pada garis g.
2. Kedudukan titik terhadap bidang
Sebuah titik dapat terletak di sebuah bidang atau di luar bidang. Jika titik terdapat di sebuah bidang maka jarak titiknya 0 dan jika titik terletak di luar bidang jaraknya dihitung tegak lurus terhadap bidang.

Contoh, pada gambar di atas diketahui sebuah titik P terhadap bidang v. Titik P diluar bidang v sehingga memiliki jarak terhadap bidang v sejauh garis tegak (P ke P’) dimana P’ merupakan proyeksi tegak lurus titik p pada bidang v.
3. Kedudukan garis terhadap garis
Dua buah garis dapat dikatakan sebagai berikut :
- Berpotongan, jika kedua garis bertemu di sebuah titik
- Berhimpit, jika seluruh titik yang dilewati garis g juga dilewati garis h
- Sejajar, jika kedua garis berada pada bidang yang sama dan tidak akan bertemu pada suatu titik
- Bersilangan, jika masing-masing garis berada pada bidang yang saling bersilangan tegak lurus

4. Kedudukan garis terhadap bidang
- Terletak pada bidang, jika seluruh garis berada pada bidang sehingga seluruh titik pada garis saling berhimpit dengan titik-titik pada bidang. Tidak ada jarak antara garis dan bidang.
- Sejajar bidang, jika seluruh titik pada garis memiliki jarak yang sama terhadap Misal jarak titik A di garis terhadap titik A’ di bidang adalah sama dengan jarak titik B di garis terhadap titik B’ di bidang.
- Memotong bidang, jika garis dan bidang saling tegak lurus.
 5. Kedudukan bidang terhadap bidang
5. Kedudukan bidang terhadap bidang
- Berhimpit, jika seluruh titik yang ada di bidang
berada pada bidang
.
- Sejajar, jika seluruh titik pada kedua bidang berada pada jarak yang sama.
- Berpotongan, jika kedua bidang bertemu di sebuah garis.

Contoh Soal Dimensi Tiga dan Pembahasan
Contoh Soal 1: Jarak Titik dengan Garis
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Tentukan jarak antara titik F dengan diagonal ruang BH.
Pembahasan

Jarak titik F dengan garis BH sama dengan panjang garis PF. Jika luas segitiga BHF diketahui
Luas BHF =  atau Luas BHF =
atau Luas BHF =  , maka:
, maka:
Contoh Soal 2: volume bangun ruang
Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik P dan Q berturut-turut terletak pada pertengahan FG dan HG. Perpanjangan garis BP, DG dan CG berpotongan di titik T. Tentukan volume limas T.BCD.
Pembahasan


Sudut CDT sama dengan sudut GQT maka :
Maka luas limas :
Contoh Soal 3: Sudut Pada Bangun Ruang
Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Q dan P adalah titik tengah HG dan FG. Jika 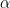 adalah sudut yang dibentuk bidang BDPQ dengan bidang ABCD maka nilai
adalah sudut yang dibentuk bidang BDPQ dengan bidang ABCD maka nilai 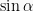 adalah ….
adalah ….
Pembahasan

Berdasarkan soal 2 diketahui 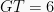 , sehingga :
, sehingga :

Dan
Maka :
Diperoleh :
Artikel: Dimensi Tiga
Kontributor: Alwin Mulyanto, S.T.
Alumni Teknik Sipil FT UI
Kontributor: Alwin Mulyanto, S.T.
Alumni Teknik Sipil FT UI

1 Komentar
mantapp bu, semangat teruss.
BalasHapus