KAIDAH PENCACAHAN
Aturan Pengisian Tempat (Filling Slots)
Aturan pengisin tempat atau dalam Bahasa Inggris disebut filling slot merupakan cara yang digunakan untuk menentukan banykanya cara suatu objek menenpati tembatnya. Contoh permasalahan mengenai aturan pengisian tempat dapat digambarkan pada masalah lima buah bola dengan warna merah, kuning, hijau, biru, dan coklat akan diletakkan pada tiga buah kotak. Kelima bola dapat diletakkan dalam beberapa posisi. Misalkan, cara pertama adalah meletakkan bola merah di kota pertama, bola kuning di kotak ke dua, dan bola hijau di kotak ke tiga. Cara lain menempatkan kelima bola dalam tiga kotak dapat dilakukan dengan meletakkan bola coklat di kotak pertama, bola merah di kotak ke dua, dan bola kuning di kotak ke tiga. Perhatikan ilustrasi dalam gambar berikut.

Mengetahui banyaknya cara untuk meletakkan lima bola dalam tiga kotak dapat dilakukan dengan cara mendaftarnya, namun hal ini pasti tidak efektif. Untuk itu, diperkenalkan cara sederhana yang dapat digunakan untuk mengetahui banyaknya cara sebuah objek dalam menempati n buah tempat. Cara ini sering disebut dengan aturan pengisian tempat (filling slots). Caranya cukup mudah, hanya dengan mengalikan kemungkinan yang dapat mengisi sebuah tempat (slot). Misalkan pada n buah tempat dengan  adalah banyaknya cara yang memenuhi untuk mengisi tempat pertama. Sedangan,
adalah banyaknya cara yang memenuhi untuk mengisi tempat pertama. Sedangan,  adalah banyaknya cara yang memenuhi untuk mengisi tempat ke-n setelah tempat pertama, ke dua, dan sebelumnya sudah terisi. Banyaknya cara untuk mengisi n buah tempat secara keseluruhan dapat diperoleh menggunakan rumus di bawah.
adalah banyaknya cara yang memenuhi untuk mengisi tempat ke-n setelah tempat pertama, ke dua, dan sebelumnya sudah terisi. Banyaknya cara untuk mengisi n buah tempat secara keseluruhan dapat diperoleh menggunakan rumus di bawah.

Agar dapat memahami penggunaan aturan pengisian tempat, simak permasalahan berikut. Dari bilangan-bilangan 1, 2, 3, 4, 5, dan 6 akan dibentuk bilangan yang terdiri atas empat angka. Syarat ketentuan yang diberikan adalah dalam empat bilangan yang akan disusun tidak boleh mempunyai angka yang sama. Contoh bilangan yang dapat disusun adalah 1.234, 3.125, 2.345, 1.345, dan lain sebagainya. Berapa banyak cara yang dapat dilakukan untuk menyusun empat bilangan tersebut? Cara mendaftar semua bilangan yang mungkin akan memakan waktu yang sangat lama. Sehingga, sangat tidak dianjurkan. Mari simak pembahasannya yang akan diuraikan di bawah.
Cara Mengisi Tempat pada Aturan Pengisian tempat
- Sediakan empat buah kotak/tempat karena kita akan menyusun sebuah bilangan yang terdiri atas empat angka. Kotak tersebut mewakili posisi bilangan yang akan dibentuk.

- Isikan angka yang memenuhi syarat untuk mengisi kotak yang disediakan. Dimulai dari kotak pertama.

- Kalikan semua angka yang mengisi tempat sesuai aturan.
Jadi, banyaknya bilangan dengan 4 digit yang disusun dari 6 angka adalah
Bagaimana? Mudah bukan penerapan aturan pengisian tempat. Kita bisa menghemat waktu sangat banyak dibanding waktu yang dibutuhkan dengan cara mendaftar. Sekarang uji pemahaman sobat tentang aturan pengisian tempat dengan menyelesaikan soal di bawah.
 
Contoh Soal dan Pembahasan
Bilangan terdiri dari tiga angka disusun dari angka-angka 2, 3, 5, 6, 7, dan 9. Banyaknya bilangan dengan angka-angka berlainan yang lebih kecil dari 400 adalah …
A. 20
B. 35
C. 40
D. 80
E. 120
A. 20
B. 35
C. 40
D. 80
E. 120
Pembahasan:
Bilangan yang akan disusun memiliki nilai lebih dari 400, sehingga nilai tertingginya adalah 397. Cara mencari banyaknya bilangan yang dapat disusun dapat dilihat seperti cara di bawah.

Jadi, bilangan tiga angka yang dapat disusun dari angka-angka 2, 3, 5, 6, 7, dan 9 dengan nilai di bawah 400 adalah  bilangan.
bilangan.
Jawaban: C
Notasi faktorial merupakan notasi operasi hitung yang ditandai dengan tanda seru (!). Notasi ini menandakan bahwa perhitungan yang harus dilakukan adalah mengalikan semua bilangan asli dari bilangan paling besarnya sampai dengan bilangan satu. Bilangan di depan notasi faktorial adalah bilangan tertingginya. Misalnya pada notasi 3!, cara menghitungnya adalah mengalikan bilangan tertingginya yaitu 3 sampai dengan bilangan 1, hasilnya adalah  . Bagaimana? mudah bukan, cara menghitung operasi hitung pada notasi faktorial. Sekarang kita lanjut ke pembahasan definisi umum untuk notasi faktorial.
. Bagaimana? mudah bukan, cara menghitung operasi hitung pada notasi faktorial. Sekarang kita lanjut ke pembahasan definisi umum untuk notasi faktorial.
Untuk setiap n bilangan asli, maka berlaku persamaan notasi faktorial di bawah.
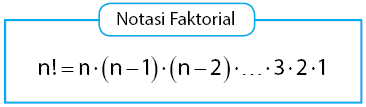
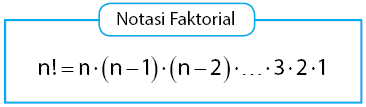
Baca Juga: Peluang Suatu Kejadian
Mengapa 1! = 1 dan 0! = 1
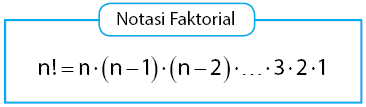
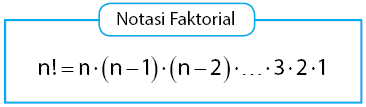
Baca Juga: Peluang Suatu Kejadian
Mengapa 1! = 1 dan 0! = 1
Suatu operasi hitung biasanya tidak akan memiliki nilai yang sama. Misalnya pada perkalian, hasil dari 0 dikali 1 tidak akan sama dengan 1 dikali 1. Hasil  dan
dan  . Atau dalam pembagian, hasil 0 dibagi 1 tidak akan sama dengan 1 di bagi 1. Hasil
. Atau dalam pembagian, hasil 0 dibagi 1 tidak akan sama dengan 1 di bagi 1. Hasil  dan
dan  . Namun, dalam notasi faktorial ada dua nilai yang sama, yaitu 1! sama dengan 0! Penasaran bagaimana bisa terjadi? Simak uraian di bawah.
. Namun, dalam notasi faktorial ada dua nilai yang sama, yaitu 1! sama dengan 0! Penasaran bagaimana bisa terjadi? Simak uraian di bawah.

Persoalan di atas dapat dijelaskan melalui penjabaran di bawah.
Jika nilai n = 1, maka akan diperoleh persamaan di bawah.
Jadi, terbuktilah bahwa nilai dari 0! = 1 dan 1! = 1. Untuk memperdalam pemahaman sobat tentang notasi faktorial, perhatikan
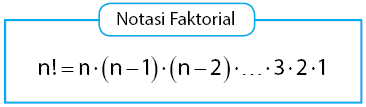 rdua contoh tentang perhitungan faktorial di bawah.
rdua contoh tentang perhitungan faktorial di bawah.
Contoh Perhitungan Faktorial
Permutasi
Permutasi mempelajari tentang menyusun k objek dari n objek dengan memperhatikan urutan. Terdapat tiga contoh permutasi yang sering muncul yaitu permutasi dari unsur-unsur yang berbeda, permutasi dengan beberapa unsur yang sama, dan permutasi siklis.
Macam-macam permutasi:
- Permutasi dari unsur-unsur yang berbeda yaitu banyaknya cara untuk menyusun k unsur dari n unsur yang berbeda.

- Permutasi dengan beberapa unsur yang sama yaitu banyaknya cara untuk menyusun unsur a dan b dari n unsur yang tersedia.

- Permutasi Siklik adalah cara menyusun n unsur yang susunannya membentuk lingkaran.

Kombinasi
Kombinasi adalah susunan yang tidak memperhatikan urutan. Contoh permasalahan yang menggunakan kombinasi adalah mengetahui banyaknya cara untuk mengambil 3 bola dari 5 bola merah dan 2 bola hijau yang tersedia dalam sebuah kotak. Cara pengambilan bola tersebut tersebut bola merah, merah, dan kuning. Cara pengambilan lain yang mungkin adalah merah, kuning merah, dan lain sebagainya. Misalkan bola warna merah tersebut diberi nomor satu sampai dengan lima dan bola kuning juga diberi nomor satu sampai dua. Cara pengambilan bola pertama berwarna merah dengan nomor dua akan sama dengan terambilnya bola warna merah dengan nomor satu. Begitu pula dengan bola dengan warna dan nomor yang berlainan. Untuk menambah pemahaman sobat idschool, perhatikan penjelasan melalui gambar di bawah.
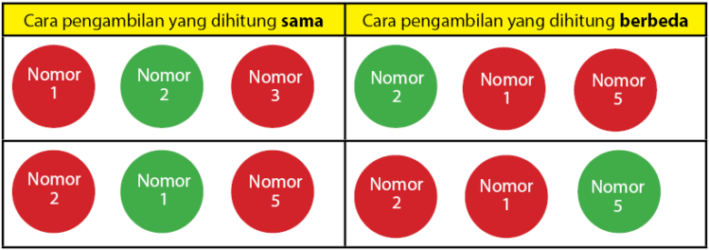
Mendapatkan jumlah banyaknya cara menyusun k objek dari n objek yang tersedia akan menghabiskan banyak waktu dan tidak efektif. Dalam ilmu peluang, ada sebuah rumus yang dapat digunakan untnuk menyusun k objek dari n objek yang tersedia. Cara tersebut adalah menggunakan rumus kombinasi. Banyaknya kombinasi k unsur yang diambil dari n unsur yang tersedia dinyatakan dalam rumus kombinasi di bawah.

Setelah mengetahui dua rumus tentang permutasi dan kombinasi, hal yang tidak kalah penting adalah membedakan permasalahan yang termasuk dalam permutasi atau kombinasi. Permasalahan yang sering muncul berupa soal cerita dan kita dituntut agar bisa membedakan masalah tersebut termasuk dalam permutasi atau kombinasi. Sehingga, tidak terjadi kesalahan dalam menggunakan rumus untuk menyelesaikan masalah tersebut. Perhatikan dua contoh kasus berikut.
Kasus pertama: permasalahan permutasi
Susunan panitia yang terdiri atas ketua, wakil ketua, sekretaris, dan bendahara akan dibentuk untuk mensukseskan suebuah acara. Susunan panitia tersebut akan dipilih dari 10 orang terpilih berdasarkan kriteria yang telah ditentukan. Berapakah banyaknya susunan panitia yang dapat dibentuk?
Susunan panitia yang terdiri atas ketua, wakil ketua, sekretaris, dan bendahara akan dibentuk untuk mensukseskan suebuah acara. Susunan panitia tersebut akan dipilih dari 10 orang terpilih berdasarkan kriteria yang telah ditentukan. Berapakah banyaknya susunan panitia yang dapat dibentuk?
Kasus ke dua: permasalahan kombinasi
Enam buku akan dipilih dari lima buku Matematika, tiga buku Fisika, dan empat buku Kimia untuk disumbangkan ke sekolah untuk anak jalanan. Berapakah banyaknya cara yang dapat dilakukan untuk memilih enam buku tersebut?
Pada kasus pertama, susunan urutan menjadi bagian yang perlu diperhatikan. Kedudukan ketua untuk orang pertama tentu akan berbeda dengan ketua yang ditempati oleh orang ke tiga. Begitu juga dengan kududukan untuk posisi lainnya. Sedangkan pada contoh kasus kedua, pemilihan buku pada urutan pertama dan kedua misalnya adalah buku Matematika pertama dan buku Matematika ke dua, keduanya merupakan buku Matematika. Sehingga, urutan tidak dipehatikan. Intinya, rumus permutasi digunakan untuk permasalahan yang memperhatikan urutan. Sedangkan kombinasi digunakan untuk menyelesaikan permasalahan yang tidak memperhatikan urutan.
Contoh Soal dan Pembahasan
Contoh soal dan pembahasan permutasi
Banyaknya susunan huruf yang dapat dibentuk dari kata NASIONAL adalah ….
A. 1.080 cara
B. 6.720 cara
C. 10.080 cara
D. 20.160 cara
E. 30.320 cara
Banyaknya susunan huruf yang dapat dibentuk dari kata NASIONAL adalah ….
A. 1.080 cara
B. 6.720 cara
C. 10.080 cara
D. 20.160 cara
E. 30.320 cara
Pembahasan:
Unsur-unsur yang sama pada kata “NASIONAL”:
N = 2, dan A = 2
Banyaknya susunan huruf yang berbeda :
Unsur-unsur yang sama pada kata “NASIONAL”:
N = 2, dan A = 2
Banyaknya susunan huruf yang berbeda :
Jawaban: C
Contoh soal dan pembahasan penggunaan kombinasi
Dalam sebuah kelas terdiri atas 7 murid perempuan dan 3 murid laki-laki. Dari kelas tersebut akan dipilih 3 orang murid secara acak, maka peluang bahwa yang terpilih ketiga-tiganya perempuan adalah …
Pembahasan:
Dalam permasalahan ini, urutan tidak menjadi hal yang perlu diperhatikan, sehingga rumus yang digunakan adalah kombinasi.
Dalam permasalahan ini, urutan tidak menjadi hal yang perlu diperhatikan, sehingga rumus yang digunakan adalah kombinasi.
Banyaknya cara untuk memilih 3 murid dari 10 murid secara acak (misalkan dengan variabel n):
Banyaknya cara untuk memilih 3 murid perempuan dari 7 murid perempuan (misalkan dengan variabel k):
Peluang bahwa yang terpilih ketiga-tiganya perempuan adalah:
Jawaban: A
Sumber : https://idschool.net/sma/aturan-pengisian-tempat-filling-slots/
Sumber : https://idschool.net/sma/aturan-pengisian-tempat-filling-slots/

0 Komentar